R data analisis
El Programa de las Naciones Unidas para el Desarrollo (PNUD) es la agencia de la Organización de las Naciones Unidas encargada de promover el desarrollo sostenible a nivel mundial, y uno de sus enfoques es la erradicación de la pobreza. En este contexto, el PNUD reconoce la importancia de abordar la pobreza multidimensional para lograr un desarrollo sostenible y mejorar el bienestar de las personas en todas las dimensiones de sus vidas.
Desde el año 2016 Chile cuenta con la medida actual de pobreza multidimensional. El propósito de esta medida es complementar la medición de la pobreza basada en ingresos con un indicador que refleje las condiciones de vida de la población en aspectos relevantes para el bienestar social y una vida digna. Desde su creación, se ha buscado obtener un diagnóstico más completo de la pobreza y contar con una herramienta útil para el diseño, implementación, monitoreo y evaluación de políticas públicas.
Inicialmente, la medida de pobreza multidimensional incluyó 4 dimensiones (Educación, Salud, Trabajo y Seguridad Social, y Vivienda) con tres indicadores por dimensión (12 indicadores en total), cada uno con igual ponderación (8,3%), por lo tanto, con dimensiones cuyo peso representan el 25% de la medida.Posteriormente, con los resultados de la encuesta Casen 2015 se incorpora una quinta dimensión de Redes y Cohesión Social y se amplía la dimensión de Vivienda para incluir el concepto de Entorno. Desde entonces, la medida ha estado compuesta por 5 dimensiones (Educación, Salud, Trabajo y Seguridad Social, Vivienda y Entorno, y Redes y Cohesión Social), manteniendo la definición de 3 indicadores por dimensión, de modo que la medida queda compuesta por 15 indicadores. Respecto del peso de las dimensiones, con el fin de favorecer cierta estabilidad de la medida, la dimensión de Redes y Cohesión Social se incorpora con un peso de 10% y se mantiene la igualdad de ponderación entre las demás dimensiones, ahora con una ponderación de 22,5%.
El objetivo de este ejercicio práctico es comprender y estimar el proceso de construcción de índices ponderados y no ponderados en R.
pacman::p_load(tidyverse, #Conjunto de paquetes, sobre todo dplyr y ggplot2
car, #Para recodificar
haven,
summarytools, #Para descriptivos
sjmisc,
psych # para Alfa de Chronbach
)
options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajoLa base de datos a utilizar es la CASEN 2022 (Encuesta de Caracterización Socioeconómica Nacional). La base de datos está disponible en este link y el cuestionario en este link.
Sin embargo, para realizar este ejercicio práctico utilizaremos una muestra aleatoria de esta base de datos para simplificar el proceso de construcción de índices. El código que crea este subset está disponible acá
load(url("https://github.com/cursos-metodos-facso/investigacion-cuantitativa/raw/main/files/data/casen2022.RData")) #Cargar base de datosview(dfSummary(casen2022, headings=FALSE, graph.col = FALSE))| No | Variable | Label | Stats / Values | Freqs (% of Valid) | Valid | Missing | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | asistencia [haven_labelled, vctrs_vctr, double] | Hogar carente en asistencia |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 2 | rezago [haven_labelled, vctrs_vctr, double] | Hogar carente en rezago escolar |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 3 | escolaridad [haven_labelled, vctrs_vctr, double] | Hogar carente en escolaridad |
|
|
9990 (99.9%) | 10 (0.1%) | |||||||||||||||
| 4 | malnutricion [haven_labelled, vctrs_vctr, double] | Hogar carente en malnutrición en niños/as |
|
|
9995 (100.0%) | 5 (0.0%) | |||||||||||||||
| 5 | sist_salud [haven_labelled, vctrs_vctr, double] | Hogar carente en adscripción a sistema de salud |
|
|
9982 (99.8%) | 18 (0.2%) | |||||||||||||||
| 6 | atencion [haven_labelled, vctrs_vctr, double] | Hogar carente en atención |
|
|
9997 (100.0%) | 3 (0.0%) | |||||||||||||||
| 7 | ocupacion [haven_labelled, vctrs_vctr, double] | Hogar carente en ocupación |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 8 | seg_social [haven_labelled, vctrs_vctr, double] | Hogar carente en seguridad social |
|
|
9945 (99.4%) | 55 (0.5%) | |||||||||||||||
| 9 | jubilacion [haven_labelled, vctrs_vctr, double] | Hogar carente en jubilaciones |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 10 | habitabilidad [haven_labelled, vctrs_vctr, double] | Hogar carente en habitabilidad |
|
|
9992 (99.9%) | 8 (0.1%) | |||||||||||||||
| 11 | hacinamiento [haven_labelled, vctrs_vctr, double] | Hogar carente en hacinamiento |
|
|
9991 (99.9%) | 9 (0.1%) | |||||||||||||||
| 12 | vivienda [haven_labelled, vctrs_vctr, double] | Hogar carente en estado de la vivienda |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 13 | serv_basicos [haven_labelled, vctrs_vctr, double] | Hogar carente en servicios básicos |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 14 | entorno [haven_labelled, vctrs_vctr, double] | Hogar carente en entorno |
|
|
9963 (99.6%) | 37 (0.4%) | |||||||||||||||
| 15 | ap_part_social [haven_labelled, vctrs_vctr, double] | Hogar carente en apoyo y participación social |
|
|
9967 (99.7%) | 33 (0.3%) | |||||||||||||||
| 16 | trato [haven_labelled, vctrs_vctr, double] | Hogar carente en trato igualitario |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 17 | seguridad [haven_labelled, vctrs_vctr, double] | Hogar carente en seguridad |
|
|
10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 18 | region [haven_labelled, vctrs_vctr, double] | Región |
|
16 distinct values | 10000 (100.0%) | 0 (0.0%) | |||||||||||||||
| 19 | area [haven_labelled, vctrs_vctr, double] | Área |
|
|
10000 (100.0%) | 0 (0.0%) |
Generated by summarytools 1.0.1 (R version 4.3.2)
2024-05-07
En esta base de datos, las variables de interés que están presentes (ej. asistencia, rezago, escolaridad) son variables dummy, es decir, variables que tienen como valores posibles 0 y 1. Donde 0 implica la ausencia de un atributo y 1 la presencia del mismo atributo.
Para medir pobreza multidimensional, 1 indica la carencia de un servicio o cualidad, por ejemplo, se considera que un hogar es carente en escolaridad si al menos uno de sus integrantes mayores de 18 años ha alcanzado menos años de escolaridad que los establecidos por ley, de acuerdo a su edad. Por lo tanto, en la variable escolaridad 1) indica un hogar carente en escolaridad, que según nuestra base de datos corresponde a 3065 hogares (30.7% de nuestra sub-muestra).
Seleccionamos solo los indicadores que eran utilizados hasta 2014
indicadores2014 <- casen2022 %>% select(asistencia,
rezago,
escolaridad,
malnutricion,
sist_salud,
atencion,
ocupacion,
seg_social,
jubilacion,
hacinamiento,
estado_vivienda=vivienda,
serv_basicos) %>%
na.omit() %>% # Eliminar Na's
mutate_all(~(as.numeric(.))) # Convertimos todas las variables a numéricasCon la función mutate creamos una nueva variable para cada dimensión, que contenga el promedio simple de los tres indicadores correspondientes.
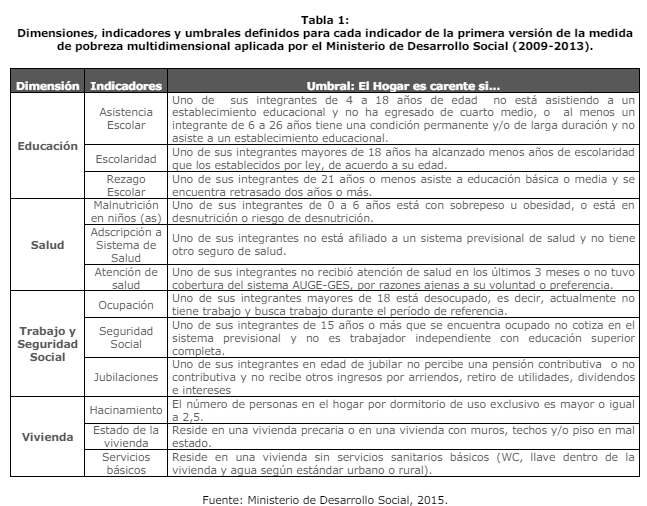indicadores2014 = indicadores2014 %>%
rowwise() %>%
mutate(educ = mean(c(asistencia, rezago, escolaridad)),
salud = mean(c(malnutricion, sist_salud, atencion)),
trabajo= mean(c(ocupacion, seg_social, jubilacion)),
vivienda= mean(c(hacinamiento, estado_vivienda, serv_basicos))) %>%
ungroup()Luego, como la pobreza multidimensional consideraba cuatro dimensiones equivalentes (sin ponderar), es posible obtener el índice de pobreza multidimensional a partir del promedio de las cuatro dimensiones.
indicadores2014 = indicadores2014 %>%
rowwise() %>%
mutate(pobreza = mean(c(educ, salud, trabajo, vivienda))) %>%
ungroup()Lo que nos da este resultado:
indicadores2014 %>% select(pobreza) %>% head(10) # Primeros 10 casos# A tibble: 10 × 1
pobreza
<dbl>
1 0.167
2 0.25
3 0
4 0.167
5 0.167
6 0.167
7 0
8 0.167
9 0
10 0.0833summary(indicadores2014$pobreza) # Resumen Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00000 0.00000 0.08333 0.10142 0.16667 0.66667 ¿Cómo podemos conocer el porcentaje total de pobreza multidimensional del país?
El PNUD considera como límite para el índice de cuatro dimensiones un 25% de pobreza multidimensional (lo que equivale a tener carencia en los tres indicadores de una dimensión). Por lo tanto, podemos utilizar un condicional que indique “si” existe pobreza muldimensional cuando nuestra variable “pobreza” sea mayor o igual a 0.25 y que indique que “no” existe pobreza multidimensional cuando la variable “pobreza” sea menor a 0.25. case_when viene en dplyr.
indicadores2014 <- indicadores2014 %>% mutate(pobreza = case_when(pobreza>=0.25~"si",
pobreza<0.25~"no")
)
prop.table(table(indicadores2014$pobreza))*100
no si
87.03161 12.96839 Según el análisis realizado con la submuestra aleatoria de la CASEN, considerando las cuatro dimensiones que se utilizaban hasta el 2014, existe un 12.97% de pobreza multidimensional en Chile
Veamos ahora el mismo proceso, pero considerando la quinta dimensión que fue agregada en 2016 sobre Redes y Cohesión Social.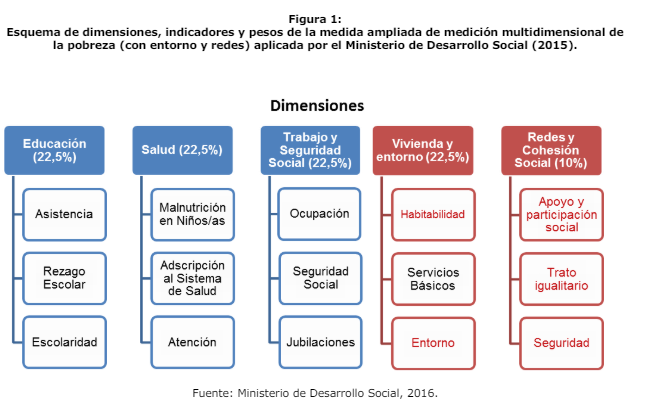
En esta operacionalización del índice de pobreza multidimensional las cuatro dimensiones originales equivalen a un 22.5% cada una, mientras que la nueva dimensión de redes y cohesión social equivale a un 10%.
Seleccionemos solo los indicadores que son utilizados desde 2016.
indicadores2016 <- casen2022 %>% select(asistencia,
rezago,
escolaridad,
malnutricion,
sist_salud,
atencion,
ocupacion,
seg_social,
jubilacion,
habitabilidad,
serv_basicos,
entorno,
ap_part_social,
trato,
seguridad,
area,
region) %>%
na.omit() %>% # Eliminar Na's
mutate_all(~(as.numeric(.))) # Convertimos todas las variables a numéricasSeguimos los mismos pasos que con el índice anterior, estimando un promedio simple para cada una de las dimensiones.
indicadores2016 = indicadores2016 %>%
rowwise() %>%
mutate(educ = mean(c(asistencia, rezago, escolaridad)),
salud = mean(c(malnutricion, sist_salud, atencion)),
trabajo= mean(c(ocupacion, seg_social, jubilacion)),
vivienda= mean(c(habitabilidad, serv_basicos, entorno)),
redes_cohesion= mean(c(ap_part_social, trato, seguridad))) %>%
ungroup()Sin embargo, como en esta ocasión se trata de un índice ponderado (con dimensiones con distinto peso cada una), multiplicamos cada dimensión por su peso correspondiente y las sumamos.
indicadores2016 = indicadores2016 %>%
rowwise() %>%
mutate(pobreza_pond = (educ*22.5) + (salud*22.5) + (trabajo*22.5) + (vivienda*22.5) + (redes_cohesion*10)) %>%
ungroup()Lo que nos da este resultado:
indicadores2016 %>% select(pobreza_pond) %>% head(10) # Primeros 10 casos# A tibble: 10 × 1
pobreza_pond
<dbl>
1 18.3
2 22.5
3 3.33
4 22.5
5 15
6 15
7 0
8 15
9 0
10 18.3 summary(indicadores2016$pobreza_pond) # Resumen Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000 3.333 7.500 10.988 15.000 62.500 ¿Cómo podemos conocer el porcentaje total de pobreza multidimensional del país?
El PNUD considera como límite para el índice de cinco dimensiones un 22.5% de pobreza multidimensional (lo que equivale a tener carencia en los tres indicadores de una dimensión). Por lo tanto, podemos utilizar un condicional que indique “si” existe pobreza muldimensional cuando nuestra variable “pobreza” sea mayor o igual a 22.5 y que indique que “no” existe pobreza multidimensional cuando la variable “pobreza” sea menor a 22.5.
indicadores2016 <- indicadores2016 %>% mutate(pobreza = case_when(pobreza_pond>=22.5~"si",
pobreza_pond<22.5~"no")
)
prop.table(table(indicadores2016$pobreza))*100
no si
84.18912 15.81088 Según el análisis realizado con la submuestra aleatoria de la CASEN, considerando las cinco dimensiones que se comenzaron a utilizar en 2016, existe un 15.73% de pobreza multidimensional en Chile.
Podemos utilizar otras variables de la CASEN para poder conocer cómo se distribuye la pobreza multidimensional en Chile. Por ejemplo, porcentaje de pobreza multidimensional por región:
prop.table(table(indicadores2016$region, indicadores2016$pobreza), margin = 1)
no si
1 0.7965261 0.2034739
2 0.7975000 0.2025000
3 0.8097345 0.1902655
4 0.8484108 0.1515892
5 0.8487230 0.1512770
6 0.8826025 0.1173975
7 0.8703170 0.1296830
8 0.8543689 0.1456311
9 0.8083736 0.1916264
10 0.7571702 0.2428298
11 0.8910891 0.1089109
12 0.9531250 0.0468750
13 0.8496241 0.1503759
14 0.8079096 0.1920904
15 0.8575198 0.1424802
16 0.8536585 0.1463415o pobreza multidimensional por zona geográfica 1) urbano 2) rural
prop.table(table(indicadores2016$area, indicadores2016$pobreza), margin = 1)
no si
1 0.8735691 0.1264309
2 0.7223301 0.2776699Para el taller práctico de hoy utilizaremos la base de datos del Estudio Longitudinal Social de Chile, realizado por el Centro de estudios del conflicto y la cohesión social COES.
El Estudio Longitudinal Social del Chile ELSOC, único en Chile y América Latina, consiste en encuestar a casi 3.000 chilenos, anualmente, a lo largo de una década. ELSOC ha sido diseñado para evaluar la manera cómo piensan, sienten y se comportan los chilenos en torno a un conjunto de temas referidos al conflicto y la cohesión social en Chile. La población objetivo son hombres y mujeres entre 15 y 75 años de edad, tiene una representación de la población nacional urbana, donde se obtuvo una muestra original de 2927 casos en el año 2016 y mantiene 1728 en 2022, además de una muestra de refresco en 2018.
El objetivo de este ejercicio del práctico es revisar el proceso de construcción y validación de escalas en R.
load(url("https://dataverse.harvard.edu/api/access/datafile/7245118")) #Cargar base de datosdim(elsoc_long_2016_2022.2)[1] 18035 750Debido a la naturaleza longitudinal de ELSOC, la base de datos contiene 18035 casos (las mismas personas durante 6 años) y 750 variables (las mismas variables en 6 periodos distintos). Por lo tanto, para simplificar el proceso de análisis de este práctico trabajaremos solo con los casos y variables de quienes participaron en la primera ola (2016)
Para el ejercicio de escalas, utilizaremos nuevamente la base de datos de ELSOC (que ya se enceuntra cargada), específicamente el módulo de Salud y Bienestar. De este módulo utilizaremos un concepto en particular llamado Estado de ánimo: sintomatología depresiva con los ítems:
Esta escala tiene solamente una dimensión, por lo que no es necesario crear objetos que contengan a cada dimensión (como vimos la clase pasada).
Filtraremos la base de datos para quedarnos con las observaciones correspondientes solamente a la ola 1, y además seleccionaremos los ítems de interés.
data2 <- elsoc_long_2016_2022.2 %>% filter(ola==1) %>% # seleccionamos solo los casos de la ola 1
select(s11_01,s11_02,s11_03,s11_04,s11_05,s11_06,s11_07,s11_08,s11_09) # items sintomatologia depresiva
head(data2) s11_01 s11_02 s11_03 s11_04 s11_05 s11_06 s11_07 s11_08 s11_09
1 5 3 3 5 4 3 3 3 1
2 2 2 3 2 3 4 3 4 2
3 2 2 3 3 4 5 4 1 2
4 1 3 3 1 1 2 3 5 1
5 1 1 1 2 1 3 1 2 1
6 1 1 1 1 1 1 1 1 1table(data2$s11_01)
-999 -888 1 2 3 4 5
5 1 1279 1196 158 192 96 table(data2$s11_02)
-999 -888 1 2 3 4 5
5 1 1302 1316 135 120 48 table(data2$s11_03)
-999 -888 1 2 3 4 5
3 1 1336 1014 179 265 129 table(data2$s11_04)
-999 -888 1 2 3 4 5
1 1 887 1414 223 261 140 Estos ítems cuentan con las mismas categorías de respuesta: (1) Nunca, (2) Algunos dias, (3) Mas de la mitad de los dias, (4) Casi todos los dias, y (5) Todos los dias. Además de los valores codificados como -888 y -999.
Recodificamos los valores -888 y -999 en NA y eliminamos los NAs.
data2 <- data2 %>%
set_na(., na = c(-888, -999)) %>%
na.omit()Dado que la escala tiene solamente una dimensión, estimaremos la correlación de toda la escala.
cor(data2) s11_01 s11_02 s11_03 s11_04 s11_05 s11_06 s11_07
s11_01 1.0000000 0.4853523 0.3737498 0.3725855 0.3574690 0.3049018 0.3021299
s11_02 0.4853523 1.0000000 0.4994332 0.5552978 0.4226467 0.4138983 0.4251018
s11_03 0.3737498 0.4994332 1.0000000 0.5592702 0.4858813 0.3902507 0.3691240
s11_04 0.3725855 0.5552978 0.5592702 1.0000000 0.5169337 0.4585532 0.4035490
s11_05 0.3574690 0.4226467 0.4858813 0.5169337 1.0000000 0.4119218 0.3685431
s11_06 0.3049018 0.4138983 0.3902507 0.4585532 0.4119218 1.0000000 0.4286404
s11_07 0.3021299 0.4251018 0.3691240 0.4035490 0.3685431 0.4286404 1.0000000
s11_08 0.3007859 0.3936463 0.3492633 0.3940693 0.3572599 0.4228090 0.5060767
s11_09 0.2347939 0.3884992 0.3026768 0.3330739 0.3040960 0.3445456 0.5080698
s11_08 s11_09
s11_01 0.3007859 0.2347939
s11_02 0.3936463 0.3884992
s11_03 0.3492633 0.3026768
s11_04 0.3940693 0.3330739
s11_05 0.3572599 0.3040960
s11_06 0.4228090 0.3445456
s11_07 0.5060767 0.5080698
s11_08 1.0000000 0.4560839
s11_09 0.4560839 1.0000000Podemos observar que todas las correlaciones son positivas, por lo que no quedaron ítems invertidos.
Primero, estimaremos la consistencia interna de cada dimensión con un Alfa de Chronbach.
psych::alpha(data2)
Reliability analysis
Call: psych::alpha(x = data2)
raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
0.85 0.86 0.85 0.4 6.1 0.0039 1.7 0.64 0.39
95% confidence boundaries
lower alpha upper
Feldt 0.85 0.85 0.86
Duhachek 0.85 0.85 0.86
Reliability if an item is dropped:
raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r med.r
s11_01 0.85 0.85 0.85 0.42 5.8 0.0041 0.0050 0.41
s11_02 0.83 0.84 0.83 0.39 5.1 0.0046 0.0062 0.37
s11_03 0.84 0.84 0.83 0.40 5.3 0.0045 0.0058 0.40
s11_04 0.83 0.84 0.83 0.39 5.1 0.0047 0.0051 0.39
s11_05 0.84 0.84 0.84 0.40 5.4 0.0044 0.0065 0.39
s11_06 0.84 0.84 0.84 0.40 5.4 0.0044 0.0072 0.39
s11_07 0.84 0.84 0.83 0.40 5.3 0.0044 0.0065 0.39
s11_08 0.84 0.84 0.84 0.40 5.4 0.0043 0.0067 0.40
s11_09 0.85 0.85 0.84 0.42 5.7 0.0042 0.0051 0.41
Item statistics
n raw.r std.r r.cor r.drop mean sd
s11_01 2888 0.62 0.61 0.53 0.49 1.8 1.01
s11_02 2888 0.74 0.74 0.71 0.66 1.7 0.85
s11_03 2888 0.73 0.70 0.66 0.62 1.9 1.13
s11_04 2888 0.77 0.75 0.72 0.67 2.1 1.07
s11_05 2888 0.71 0.69 0.63 0.59 1.8 1.07
s11_06 2888 0.68 0.68 0.62 0.57 1.6 0.96
s11_07 2888 0.67 0.70 0.65 0.58 1.4 0.80
s11_08 2888 0.66 0.68 0.62 0.56 1.4 0.85
s11_09 2888 0.58 0.63 0.56 0.50 1.2 0.61
Non missing response frequency for each item
1 2 3 4 5 miss
s11_01 0.44 0.41 0.05 0.06 0.03 0
s11_02 0.45 0.45 0.05 0.04 0.02 0
s11_03 0.46 0.35 0.06 0.09 0.04 0
s11_04 0.31 0.48 0.08 0.09 0.05 0
s11_05 0.51 0.33 0.05 0.07 0.04 0
s11_06 0.63 0.26 0.05 0.05 0.03 0
s11_07 0.72 0.21 0.03 0.03 0.01 0
s11_08 0.73 0.19 0.03 0.03 0.02 0
s11_09 0.86 0.10 0.02 0.01 0.01 0data2 <- data2 %>%
rowwise() %>%
mutate(sintomatologia_depresiva = sum(s11_01,s11_02,s11_03,s11_04,s11_05,s11_06,s11_07,s11_08,s11_09))
summary(data2$sintomatologia_depresiva) Min. 1st Qu. Median Mean 3rd Qu. Max.
9.00 11.00 14.00 14.99 17.00 45.00 ¿Tiene sentido una escala de 9 a 45? No, por eso generalmente se recomienda que las variables ordinales partan en ‘0’ para que el comienzo de la escala también sea 0. En ese caso, deberíamos recodificar las 9 variables en una escala de 0 a 4.